

It was immediately recognized that if Thurston’s conjecture were true, then the Poincaré conjecture must be true as well. In the late 1970’s, William Thurston of Princeton University made an exceptionally bold conjecture about the geometry of all three-dimensional spaces. Though the statement of the Poincaré conjecture is simple enough, a proof has eluded mathematicians for the past hundred years in spite of intensive efforts by many talented mathematicians. This conjecture is, in many respects, the beginning point of any study of three-dimensional spaces.
The Poincaré conjecture says, plainly enough, that the three-dimensional sphere, the set of points in four-dimensional space that are a constant distance from the origin, is the only simply connected three-dimensional space. In fact, an old theorem in topology tells us that the surface of the basketball, known to topologists as the two-dimensional sphere, is the only surface that is simply connected. For instance, if the string winds around the hole in the bagel, the loop will never disappear when pulled on. However, if we perform the same experiment on the surface of a bagel, this is no longer true. Because it possesses this property, the surface of the basketball is called “simply connected.” No matter how the string is laid out, we can make the loop disappear by pulling it through the slip-knot. Imagine that we take a piece of string tied in a loop with a slip-knot and arrange it on the surface of a basketball.
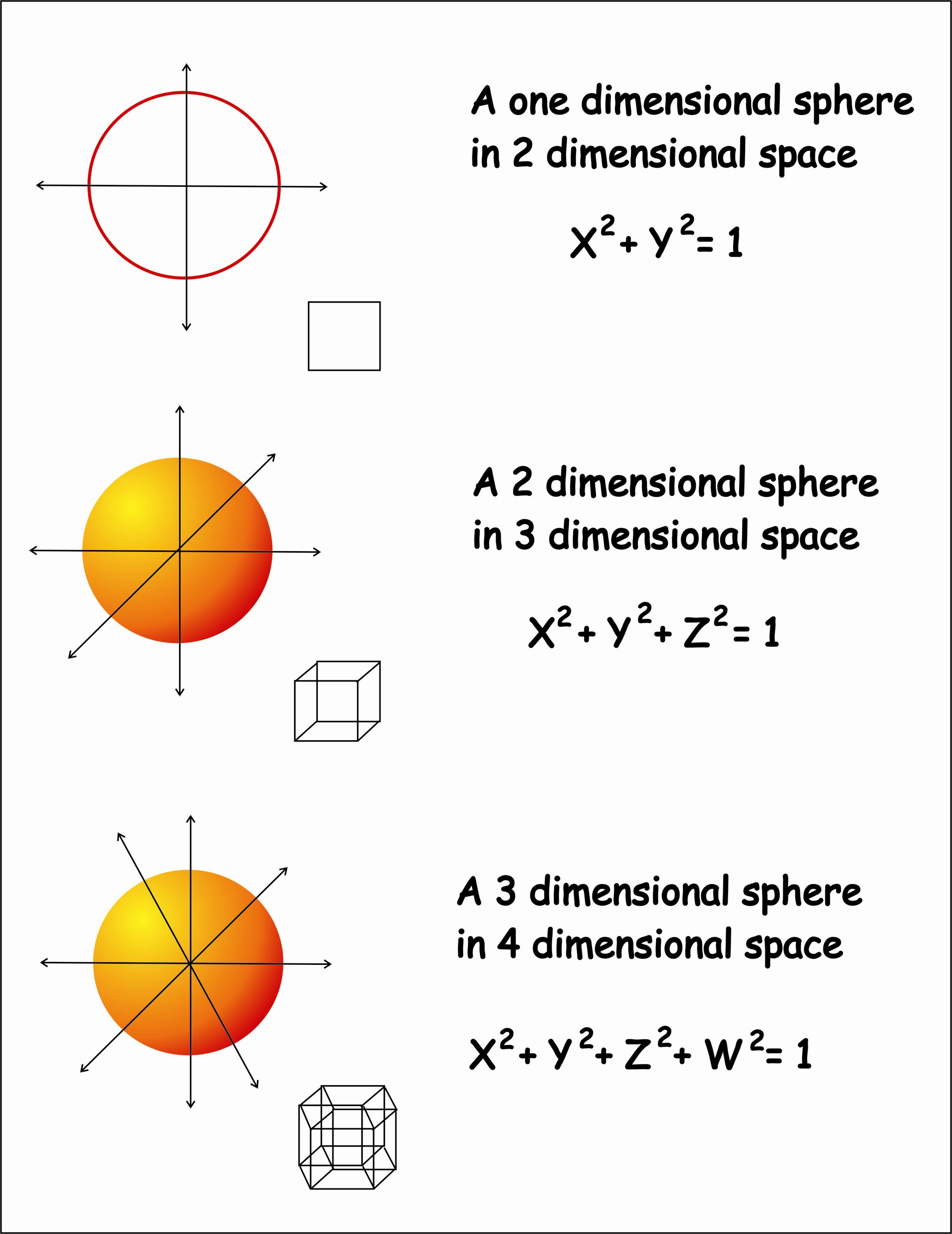
To understand what it says, let’s first think about a two-dimensional analogy. The Poincaré conjecture deals with the structure of three-dimensional space. Recent work of Grigori Perelman, a Russian mathematician working at the Steklov Institute of Mathematics, seems to give a solution to one of these problems, the so-called Poincaré conjecture, a problem in topology first posed in 1904. Rather than offering a good grade, however, the institute offers $1 million for the solution of just one of these problems. Remember all the hours you spent working on your Math 210 proof portfolio in the hopes of earning a respectable grade? The Clay Mathematics Institute has published a portfolio of seven mathematics problems for the mathematical community.


 0 kommentar(er)
0 kommentar(er)
